The optimization set: Non-linear solvers

This log will focus on open methods for solving non-linear equations, including fixed-point iteration, Newton-Raphson method, Bairstow’s method, Quotient Difference algorithm and Muller’s method.

Open? Close?
General functions
Polynomials
- Bairstow's method (for complex roots)
- Quotient-Difference Algorithm
Quadratic Interpolation
- Muller's method

Slides reference: Prof. Sun, Peng – Non-Linear Equation Solvers

Textbook reference: Numerical Methods for Engineers SEVENTH EDITION

Open? Close?

The “close” methods are actually called bracketing methods. For these methods, we start with an interval that brackets the root. Then, we utilize properties of the target function to narrow down the interval iteratively. Typical examples of bracketing methods include the bisection method and the false position method.

Open methods, one the other hand, starts the iteration with a single starting value of x or two starting values that do not “bracket” the root. Because of this, they can sometimes diverge from the true root. However, when they converge, they usually do so much more quickly than bracketing methods.

General functions

Simple fixed-point iteration

Description

For a function $f(x) = 0$ , we rearrange the function in the form of $x = g(x)$ such that $g(x) = f(x) + x$ .

In the case of $f(x) = x^2 - x - 2 (x>0)$ , there are 3 different ways to rearrange them：

$x = x^2 - 2$
$x = \sqrt{x + 2}$
$x = 1 + \frac{2}{x}$

Algorithm

Given a initial guess of the root $x_i$ , the guess is updated iteratively: $x_{i+1} = g(x_i)$ .

We also need a indicator to evaluate the convergence and to decide when to stop the iteration. The following error indicator serves this purpose:

$\varepsilon_a = \abs{\frac{x_{i+1}-x_{i}}{x_i}}100\%$

Convergence

One way to check whether the algorithm will yield convergent results is the two-curve graphical method.

For the function $f(x) = e^{-x} - x$ , we rearrange into the form of $e^{-x} = x$ . If we plot $e^{-x}$ and $x$ respectively, then the intersection of the two curves represents the root we are looking for. The graph allows us the visualize the iterations as follows (It is easy to see that the algorithm converges!):

From this graphical perspective, we can also derive the sufficient condition for convergence is $\abs{g'(x)} < 1$ . The following is the proof:

Note that $x_r - x_{i}$ is the error for step $i$ and $x_r - x_{i+1}$ is the error for step $i+1$ . If we want the algorithm to converge, we want the error at step $i+1$ smaller than the error at step $i$ . Hence, a sufficient condition for convergence is $\abs{g'(x)} < 1$ .

An offshoot of the analysis is that it also demonstrates that when
the method converges, the error is roughly proportional to and less
than the error of the previous step. For this reason, simple fixed-point
iteration is said to be linearly convergent. (Taken from textbook)

Aitken acceleration

Aitken acceleration will improve the convergence speed from linear to quadratic in ideal condition (which satisfies the ”geometric series’ like assumption).

We define:

Then the acceleration scheme becomes:

Newton-Raphson method

In fixed-point iteration, the only property from the target function is that local values of $f(x)$ given a certain $x$ . Therefore, another direction to improve the convergence speed is trying to utilize more properties from the target function $f(x)$ . This is exactly what we do in the Newton-Raphson method,

In the Newton-Raphson method, we use the information of derivatives. The following graph gives a good geometric intuition.

Update rule

The first derivative at $x$ is equivalent to the slope:

$f'(x) = \frac{f(x_i) - 0}{x_i - x_{i+1}}$

which can rearranged to yield:

$x_{i+1} = x_{i} - \frac{f(x_i)}{f'(x_{i})}$

Taylor series

Pitfalls

Just as every other open method, the Newton-Raphson method come with no guarantee of convergence. This diagram depicts the four common pitfalls that would lead to slow convergence/divergence of the method.

(a): Divergence: Inflection point in the vicinity of the root, i.e., $f''(x) = 0$
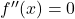
(b): Root-jumping: Near-zero slope encounter
(c): Oscillations: Iterations can oscillate around a local minima or maxim
(d): Division-by-0: Zero slope

To deal with these potential pitfalls, we can:

Test with multiple initial values
Adopt a hyperparameter 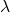$\lambda$ to scale the step (the “learning rate”):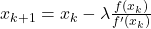 $x_{k+1} = x_k - \lambda \frac{f(x_k)}{f'(x_k)}$
And always remember to set the max iteration!

Secant method

The secant method is useful for the cases where the first-order derivatives cannot be computed analytically – a requirement for the Newton-Raphson method.

Update rule

Start with two values: $x_1$ and $x_2$

You may find that the secant method is not that different from the Newton-Raphson method. Basically, it adopts additional estimation for the first order derivative.

Polynomials

To be honest, this section is considerably more complex but not complicated. I really don’t have energy to cover everything and I don’t find it fit to include too much details in the log. So please refer to the slides attached on this section.

Bairstow’s method (for complex roots)

Quotient-Difference Algorithm

Quadratic Interpolation

Muller’s method

A quadratic interpolation method – using parabola to fit the curve (Compare with Newton-Raphson and false position – these are linear interpolation methods. The ideas are actually similiar.)