The optimization set: Convex optimization

Convex optimization problem
Convex function
Duality – Convert for ease

This log will cover one of the most important optimization problems: the convex optimization. We will look at the math derivations in detail and get some hand-on practice.

Reference: Convex Optimization – Boyd and Vandenberghe; Slides from Prof. Sun, Peng’s MATH304 course at DKU.

Convex optimization problem

Convex function

Geometrically, it is helpful to visualize every point on the function as the endpoints of the vectors $(x_0, f(x_0))$ . The basic equality involved in this definition is also called Jensen’ inequality.

At the same time, the extended-value definitions gives us a simpler expression:

When checking if a function is convex/using the convex conditions, we don’t have to use the original definition all the time. Instead, we can use the first-order conditions and the second-order conditions. Both are necessary & sufficient conditions for convex functions.

First-order conditions

We utilize the first-order Taylor expansion for the first-order conditions:

Suppose $f$ is differentiable. Then $f$ is convex if and only if $dom f$ is convex and

$f(y) \ge f(x) + \nabla f(x)^T(y - x)$

holds for all $x, y \in dom f$

The graph below visualizes the first-order conditions. Note that the $\nabla f(x)$ is reduced to simply $f'(x)$ in the 1-D case:

For the special case where $\nabla f(x_0) = 0$ , then for all $y \in dom f$ , $f(y) \ge f(x)$ . This suggests that $x_0$ is in fact a global minimizer of the function $f$ .

Second-order conditions

Just like the first-order, the second-order conditions utilize the second-order Taylor expansion.

The following proof tells us why the positive semi-definite condition must hold for ALL $x \in dom f$ :

Example

With the definitions above, we can practice on checking the convexity of a few problems!

Least-square objective: $f(x) = ||Ax - b||_2^2$

(Reference: Hessian on linear least squares problem – Mathematics Stack Exchange)

First, we want the find the Hessian matrix:

We observe that $f(x) = g(h(x))$ , where $h(x) = Ax - b$ and $g(y) = \frac{1}{2} ||y||^2$ . Therefore, we can apply the chain rule:

$\nabla f(x) = A^{T}(Ax - b)$

Then we can take the second derivative to find the Hessian:

$Hf(x) = A^{T}A$

Furthermore, we know that $A^{T}A$ is positive semi-definite, since for any vector $x$ we have:

$x^T(A^TA)x = (Ax)^T(Ax) = ||Ax||_2^2 \ge 0$

Now you can see why the least square problem is a special case of convex optimization problems!

(Note: on the relationship of positive semi-definite and eigenvalues, refer to: linear algebra – Prove that every positive semidefinite matrix has nonnegative eigenvalues – Mathematics Stack Exchange)

Quadratic functions

Other common examples of convex functions

Practical methods for determining convexity

Duality – Convert for ease

The Lagrangian (Step 1)

The Lagrangian Dual Function (Step 2)

(Extended reading: Understanding Duality and Lagrangians in Optimization | MLDemystified)

The dual function $g(\lambda, \nu)$ is the pointwise infimum of a family of affine functions of $(\lambda, \nu)$ . Therefore, $g(\lambda, \nu)$ is concave, even when the original problem is not convex (Since we are taking the pointwise infimum on $x$ , we can treat the functions containing $x$ as constants).

Here is the most important takeaway: The dual function gives us an lower bound for the original optimization problem.

Below are two examples on constructing the dual problems:

Standard form LP

Least-norm solution of linear equations

The dual problem

Week & Strong duality

Recall that $p*$ is the optimal solution for the original problem, while $d*$ is the optimal solution for the dual problem.

Weak duality: $p* \ge d*$
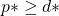
Strong duality: $p* = d*$

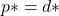
Strong duality is a favorable condition, as solving the dual problem (which is usually easier) will give us the solution for the original problem. One of the sufficient condition for strong duality is Slater’s constraint qualification.

Example: Quadratic problem

During the derivation, we will encounter the following expression:

$(P^{-1})^{T}P$

Recall that in the problem definition, the matrix $P$ is required to be positive semi-definite, which implies that P is a symmetric matrix. Therefore:

$(P^{-1})^{T}P = I$

(I personally missed this point when doing the derivation myself, so I decide to add a note here)

Example: A non-convex problem with strong duality

Geometric interpretation of duality

Always bear in mind the range of $u$ ( $u \preceq 0$ ) when going through these visualizations.

Complementary slackness

(Important assumption!) Strong duality holds, $x^*$ is primal optimal, and $(\lambda^*, \nu^*)$ is dual optimal, we have:

We call the condition

$\lambda_{i}^*f_{i}(x^*) = 0, i = 1 ... m$

Complementary slackness

KKT Conditions

KKT conditions give us a way to rewrite primal optimization problems with differentiable $f_{i}, h_{i}$ and strong duality. This form can make the problem easier to solve under some circumstances. Note that the primal problem is not necessarily convex.

Example: Equality constrained convex quadratic minimization

The optimization set: Convex optimization

Convex optimization problem