Modern diffusion models, like Stable Diffusion 3 and flux, have changed their basic model structure to flow-based models. Understanding flows is crucial and yet challenging. In this article, we try to decode flow-based diffusion modes with Rectified Flow, one of the most elegant solutions. Note that this article aims to explain the concepts from a relatively high level, and detailed proofs can be found in the original paper.
Problem
Given distribution ![]() , want to find a transfer map
, want to find a transfer map ![]() such that:
such that:
![]()
Example: ![]() is a Gaussian,
is a Gaussian, ![]() is the target distribution.
is the target distribution.

Math
(In understandable language)
- Vector field
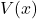 : A vector field defined in
: A vector field defined in 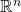 that indicates the direction and magnitude at each point
that indicates the direction and magnitude at each point 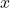 .
. - Velocity field
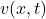 : A special type of vector field that indicates the rate of change and tangent direction of each point
: A special type of vector field that indicates the rate of change and tangent direction of each point 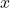 . Here,
. Here, 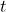 represents the time step.
represents the time step.
Method:
Rectified Flow
We learn ![]() implicitly by constructing an Ordinary Differential Equation(ODE):
implicitly by constructing an Ordinary Differential Equation(ODE):
![]()
Intuitively, the best way to get ![]() from
from ![]() is to have a “straight” flow.
is to have a “straight” flow.

So we need to find an ODE to match the linear interpolation of points from ![]() and
and ![]() .
.
Observe ![]() ,
, ![]() . Let
. Let ![]() for
for ![]() be the linear interpolation of
be the linear interpolation of ![]() and
and ![]() :
:
![]()
We can have a trivial ODE:
![]()
- Note that this ODE is not causal or forward simulatable, as we need to know
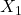 when
when 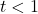 in order to calculate
in order to calculate 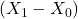 .
.
So we want our ODE ![]() to be as close as possible to the trivial ODE.
to be as close as possible to the trivial ODE.
A simple way is to optimize ![]() by minimizing:
by minimizing:
![]()
![]()
And ![]() can simply be a neural network.
can simply be a neural network.
Reflow: Straight Flows

The method above gives us the flow (b). In order to get flow (c), we can do:
![]()
![]()
We call it 2-rectified flow.
- Note that we can do such a process multiple times.
- Always remember the Reflow process can speed up the generate process, and will not improve the generation performance.
发表回复